In this article, we will explore how shared key exchange works. If you’re completely new to the concept of VPNs, check out this introduction.
Getting Started with VPNs
This article is part of a series on VPNs. If you already know a little about the how VPNs work and want to know a little more, this series is for you. Each article addresses one aspect of how a VPN helps secure data by telling a story that serves as a metaphor for the logical mechanisms involved.
Shared Key Exchange
In earlier adventures, our friends Adam and Burt have tried to keep their comic book project secret from Cesar’s snooping by securing the messages they exchange with a shared key and a more elaborate public-/private-key pair system. Each system has its strengths and weaknesses. But the boys need a break from this project, and lucky for them, there’s a fair going on nearby. They enter the chili cook-off, and because they love keeping their creations secret, they devise a way of keeping their recipe secret, even as they prepare it in front of onlookers. The recipe will be so secure; even they won’t know it!
A Well-Known Starting Point
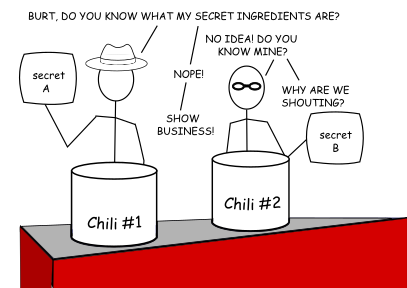
To pull this feat off, Adam and Burt will each need to develop a portion of the recipe without knowing anything about what the other has contributed. If neither of them knows the whole recipe, neither can reveal it. However, they agree on a common base of ingredients (a mixture of tomato base, chili seasoning, beef, and beans). There’s no need to keep this part secret–most of the other contestants start with a similar base, so they gain little in spending the effort to obscure these ingredients.
Negotiating the Key Exchange
The fact that the two parties can start with this negotiation over an insecure, public medium is one of the core and clever ideas behind this method of initiating encryption. Before any encryption can occur, there needs to be some unencrypted traffic between peers, otherwise, neither will know how to decrypt any future messages. This initial step lets one host tell another that it wishes to begin a negotiation of an encryption method by offering a couple of initial values to a well-known mathematical formula (which, in this example, is the base of the chili). The real magic comes in the next steps.
Seeding the Key
Adam and Burt have independently and secretly prepared a portion of seasoning and additional ingredients sealed in an opaque, rice-paper pouch that will dissolve once immersed in the chili. In this cook-off, Adam’s pouch contains tomatillos, chipotles, cayenne pepper, and cinnamon; Burt’s has Cajun seasoning, beer, cumin, oregano, and Worcester sauce*. Adam tosses his packet into his pot and stirs, tasting his chili until he is sure the pouch has dissolved and released its ingredients. Burt does the same with his pot. At this point, Adam and Burt have two different chilis.
*(in case you are wondering why this isn’t already dissolving from the beer, let’s say that Burt has pre-frozen any liquids before placing them in the dissolvable pouch.)
Generating the Shared Key
In the actual key exchange process, these “ingredients” are actually very large prime numbers. In the key-exchange process, these large prime numbers are randomly generated. The larger the numbers used to input into this key exchange, the more difficult it is to use brute-force techniques to crack. The size of these numbers is called a bit group. A group of prime numbers of the same length in binary bits (e.g., 1024 or 2048 or even larger bit lengths) all belong to the same group. The larger the bit group, the more robust this key exchange process becomes and the more resistant it becomes to analysis and potential compromise.
Completing the Exchange
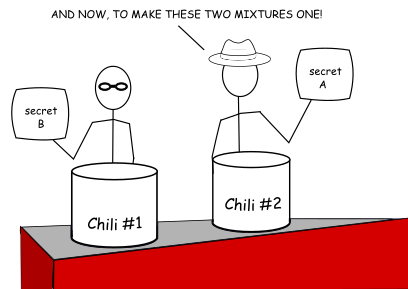
Now they switch the pots they are tending to, so Burt is at the pot Adam started, and vice versa. They each take another pouch identical to the one they started with and add this second pouch to the pot that the other had started (so Adam adds his tomatillos, chipotles, cayenne pepper, and cinnamon to the pot Burt started with the Cajun seasoning, beer, cumin, oregano, and Worcester sauce; and Burt adds his pouch to the pot Adam started). After each of them stirs their respective pots and dissolves the pouches to release the secret ingredients, they can be sure that each pot now contains identical chilis.
The Diffie-Hellman Key Exchange
In mathematical terms, the algorithm governing shared key exchange is commutative–it can be performed in any order and get to the same result. Also, note that neither Adam nor Burt have the means to reconstruct the key alone. Each of them only know the random value each contributed to the algorithm. And, since each also generates a copy of the key upon completion of the negotiation, each also has a copy of the final key without its having had been transmitted over a network.
This shared key exchange or negotiation is called the Diffie-Hellman Key Exchange, named for the authors of the paper that first detailed this method, Whitfield Diffie and Martin Hellman. Their work built upon previous work done by Ralph Merkle, so it has been suggested (by Hellman himself) this method be called the Diffie-Hellman-Merkle Key Exchange. In actual configurations, you will often see this method applied as DH Groups, different groups corresponding to keys of different lengths in binary bits.
Complex Tastes
During the preparation, any judges could have seen and sampled from the starting pots or the intermediate pots. Even if Cesar, intent on learning the secret recipe, poses as a judge, he wouldn’t be able to reliably reconstruct the final recipe Adam and Burt used. (This example assumes that Cesar doesn’t have the ability to distinguish all the individual flavors included in the chili. To attempt to identify the ingredients and their amounts via laboratory analysis would be expensive enough in time and energy invested in making it infeasible.)
Potential Vulnerabilities
If an attacker wanted to compromise any communication encrypted with this key, a typical man-in-the-middle eavesdropping attack would be insufficient. An attacker could, however, insert himself as a transit man-in-the-middle. If an attacker set himself up so that all communication between the two hosts had to go through him, he could perform a Diffie-Hellman negotiation with each peer. Each side of the connection would only know whether a successful key is negotiated, but not with whom. In this position, the man-in-the-middle would be able to see the whole conversation–in fact, he’d have to decrypt incoming traffic and re-encrypt it before sending it out the other side to maintain the impression that each end still has its “secure” connection.
It’s also possible for an attacker to attempt to stage a man-in-the-middle attack to downgrade the DH group to a group whose bit length is much smaller and less secure. That attacker could then collect the weakly encrypted data and perform an offline brute force attack against the encryption to crack it in a reasonable amount of time. Attacks such as FREAK and Logjam use some sort of downgrade methodology to weaken the Diffie-Hellman key exchange.
More in the How VPNs Work Series
Part 1: Symmetrical Encryption Algorithms
Part 2: Public Key Cryptography
Learn more about our VPS hosting services and VPS hosting prices.