What is Public Key Cryptography (How VPNs Work, Part 2)
May 13, 2015 by Mason Moody ( 5 ) under VPS Hosting
0 Comments
This article in the “How VPNs Work” series describes how public key cryptography (asymmetric encryption) works. If you’re already lost, don’t panic! This series of articles is written to explain the concepts and methods behind VPNs without requiring a deep dive into the mathematics that powers them.
If you’re completely new to the concept of VPNs, check out this introduction. If you already know a little about the how VPNs work and want to know a little more, this series is for you. Each article addresses one aspect of the means by which a VPN helps to secure data by telling a story which serves as a metaphor of the logical mechanisms involved. These stories involve two people, Adam and Burt, trying to keep a secret and a third person, Cesar, trying to nefariously discover their secret. Since VPNs have no perfect physical world equivalent, there may be some elements that stretch the bounds of credibility (for example, Cesar has access to a duplicator ray). Remember, it’s just a story…
Each article also has expandable sections (indicated with the gear icon) which contain a slightly more in-depth explanation that is somewhat more technical but still avoids getting too lost in the mathematics. These sections tie the events of the story a little more to the components or steps of encryption or authentication but are not required to get a basic understanding of the topic.
Adam and Burt have already discovered the weakness in using a lockbox with a shared symmetric key to keep things secure. So, Burt proposes they try a new method in which each of them has their own unique set of keys (asymmetric encryption).
Public Key Cryptography
Public Key Cryptography is an asymmetric encryption methodology that seeks to maintain confidentiality without having to ever share a secret key over an insecure channel (such as unencrypted email). In this explanation, Adam and Burt each have a unique lock, but for the remainder of this example, we’ll cover Burt’s lock and keys (Adam’s lock and keys will work in the same fashion). Each lock has two special properties: first, the lock has two distinct and related keys that can work with it, and second, each key that works with the lock can only turn in the lock in one direction–for the sake of this example, they only turn clockwise.
Paired Keys
These keys are, in actual use, called the public and private keys (the color designations are to help make the explanation a little easier to follow). The generation of these keys involves some pretty nifty and complicated mathematics. (These algorithms begin with calculations involving the product of two very large prime numbers and is far beyond the scope of this example.) Common algorithms used in public key cryptography include RSA (named for its creators, Rivest, Shamir, and Adleman), DSA/DSS (Digital Signature Algorithm/Digital Signature Standard), and ECDSA (Elliptic Curve Digital Signature Algorithm). This latter algorithm instead utilizes the mathematics around elliptic curves and is at least as intimidating to the math-averse as the RSA algorithm.
The Clockwise Lock (How the Keys Work)

In this fashion, when the lock is secured with the green (public) key, only the person who possesses the red (private) key can open it. This is how Burt can make the green key widely available to the public. He can send a copy of the green key to Adam (he could even make a copy available for public pickup or duplication). Anyone who has a copy of this green key can lock this lock, and at that point, only Burt–assuming he keeps his red (private) key secure–can open the lock. Now, when Adam wants to securely send something to Burt, he can use Burt’s green (public) key. Similarly, Adam would have his own key pair, and he could also make his green key available for Burt (or anyone else) to use.
Now, if our ne’er-do-well Cesar were to try to crack this method of security, he’d need to crack two different locks in order to get the whole conversation. Even if he were able to get past just one, he’d only be able to see one half of the conversation.
This usage of one-way encryption is employed in some secure email exchanges, such as with the use of PGP (Pretty Good Privacy) or GPG (Gnu Privacy Guard). If you’ve ever seen mention of someone’s PGP or GPG public key (and likely a block of random-looking text that was the key itself), you can see why it can be published as a part of an email signature or a publicly accessible website. With that key, anyone can encrypt an email that only the possessor of the private key (the recipient) can decrypt.
A Twice-Locked Box
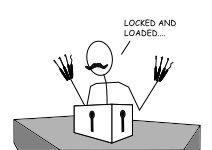
Adam, not having a copy of Burt’s red (private) key, can’t unlock the lock. But he can place his own lock on the box. He secures this lock with his own green (public) key. Adam sends this twice-locked box back to Burt.
Burt gets the box, and the only way he can open it is if he has both his own red key and Adam’s red key. But Adam is keeping his red key just as secret as Burt keeps his own red key, so Burt won’t be able to open the box. Burt, though, doesn’t want to open the box–remember, he started this process, so he wants Adam to get the art contained within the box. He can, though, unlock his own lock with his own red (private) key. When he does this, the only security on the box is the lock that Adam secured.
Burt sends the box back to Adam, and now Adam, using his red key, unlocks the remaining lock. Burt has successfully and securely sent this package. This method adds a couple of layers of security, in that there are two layers of locking/encryption and in the fact that no shared key needs to ever be exchanged via a potentially insecure medium. However, it isn’t a very efficient system if they need to send more secure messages back and forth in a more timely manner.
This ability is one of the interesting features of the mathematics behind public key cryptography. A message can be encrypted multiple times; then, when decrypting it, that decryption can be done in any order. It works in a commutative way the way some simple mathematic functions work. For example, if you were to start with the number 10 and add three other numbers–say, 3, 5, and 7 (so, 10 + 3 + 5 + 7 to get 25), you could then subtract them from your total in any order to get back to the same original number (25 – 5 – 7 – 3 = 10). Of course, the mathematics behind this cryptography is significantly more intricate.
A Complicated, Robust Lock
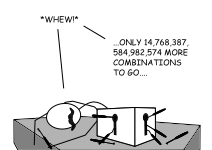
There is, however, one advantage to this inefficiency. If Cesar were to use a device that could simulate any key, and assuming that to open one of these locks requires the full 10 rotations just to see if that key works, then the time it would take him to try every key combination (a brute force attack) goes up by a factor of 10 as well.
The length of an encryption key is measured in bits. The larger the bit length of the key, the more resistant that key is being discovered via brute-force cracking attempts. The larger the bit length of the key also means that the work required to perform encryption or decryption increases. However, since asymmetric and symmetric encryption algorithms work in different ways, their key lengths aren’t directly comparable. For example, an RSA (asymmetric) 1024-bit key has about the same strength as an 80-bit symmetric key. There are tools available to compare relative key lengths across the different encryption methods, such as the one maintained by BlueKrypt, that can help illuminate the difference in computational cost between these methods.
These differences highlight one of the primary conundrums of computer security: security vs. convenience. Work done to improve one often comes at the expense of the other. Increasing the bit-length of the encryption key increases its strength, but it also means that it will take longer to perform that encryption and decryption. When measures are made to improve convenience, such as increasing computing power or reducing the length of the key, those same measures also mean it requires less work to successfully guess the key through brute-force methods.
More in the “How VPNs Work” Series
Part 1: Symmetrical Encryption Algorithms
Part 3: Shared Key Exchange
Learn more about services from Atlantic.Net, including VPS hosting.
Get a $250 Credit and Access to Our Free Tier!
Free Tier includes:
G3.2GB Cloud VPS a Free to Use for One Year
50 GB of Block Storage Free to Use for One Year
50 GB of Snapshots Free to Use for One Year
